8.3 KiB
回溯算法
1、八皇后问题
1.问题描述
在8×8格的国际象棋上摆放八个皇后,使其不能互相攻击,即任意两个皇后都不能处于同一行、同一列或同一斜线上,问有多少种摆法!
2.分析
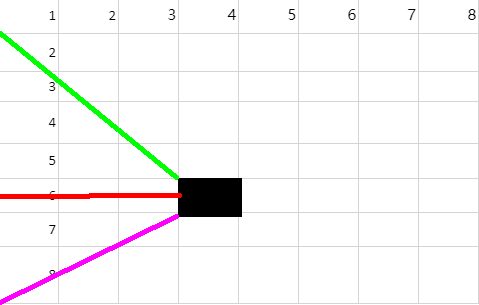
假设我们此时要在黑色方块的位置上面放置一个皇后:
如果一列一列的放置皇后的话,图中黑色位置能放置一个皇后的合法性条件为: 1、绿色线条经过的方格没有皇后 (不处于同一斜线) 2、红色线条经过的方格没有皇后 (不处于同一行) 3、紫色线条经过的方格没有皇后 (不处于同一斜线)
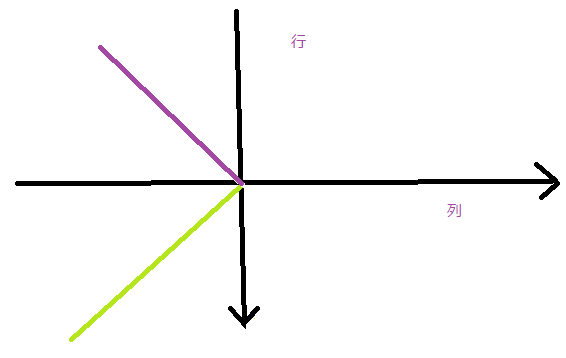
也就是说以一列一列的放置的话,黑色的为起点(0,0)坐标点,紫色和绿色两个线条分别是斜率为1和-1的两个函数,如下图: 紫色线所代表的函数是:y = -x; 绿色先所代表的函数是:y=x; (横坐标是列,纵坐标为行,注意行从上到下递增)
凡是位于这两条函数线上的位置(点)以及横坐标(说明位于同一行)都不能有皇后
所以假设某一列皇后的位置用行来记录,比如queen[column] = row,意思是第column列的皇后的位置在第row行。 同行的逻辑很好判断,那么我们想要在黑色方块位置放置一个皇后,怎么判断前面几列是否在绿色线条和紫色线条上已经有了皇后呢?思路也很简单:
假设黑色方块的位置为n列,nRow行,假设位于m列的所在的行是否有皇后位于紫色线或者绿色上,那么就符合下面条件:
//假设此时即将在n列放置一个皇后,n>m
//获取m列上皇后所在的行
int mRow = queen[m]
int nRow = queen[n];
//行的差值
int rowDiff = nRow - mRow;
//列的差值
int columnDiff = n-m;
这个代码中 rowDiff的绝对值等于columnDiff的绝对值的话那么就说明点位于y=x或者y=-xd 函数上面
就说明此时的合适方块的位置是不能在放置皇后了,因为绿色或者紫色上面已经存在皇后了。那么使用代码来判断就是
public boolean isLegal(int currentRow,int currentColumn) {
//遍历前面几列
for(int preColumn=0;preColumn<currentColumn;preColumn++) {
int row = queen[preColumn];
//说明在子preColumn的低currentRow已经有了皇后
if(row==currentRow) {
return false;
}
//行与行的差值
int rowDiff= Math.abs(row -currentRow);
//列于列的差值
int columnDiff = Math.abs(currentColumn-preColumn);
//说明斜线上有皇后
if(rowDiff==columnDiff ){
return false;
}
}//end for
//说明(currentRow,currentColumn)可以摆放。
return true;
}
这是按照一列一列的方式来进行放置的,所以整体思路就是:在当前列逐步尝试每一行是否可以放置皇后,如果有一个可以放置皇后,就继续查看下一列的每一行是否可以放置皇后
int queen[] = new int[8];
int count = 0;
private void eightQueen(int currentColumn) {
//这个for循环的目的是尝试讲皇后放在当前列的每一行
for(int row=0;row<8;row++) {
//判断当前列的row行是否能放置皇后
if(isLegal(row,currentColumn)) {
//放置皇后
queen[currentColumn] = row;
if(currentColumn!=7) {
//摆放下一列的皇后
eightQueen(currentColumn+1);
}else {
//递归结束,此时row要++了
count++;
}
}
}//end for
}
需要注意的是当currentColumn==7的时候,说明此时已经完成了一种摆放方法,然后for循环继续执行,去尝试其他摆放方法。 测试一波,一共有92种摆放方法:
public static void main(String args[]) {
EightQueen queen = new EightQueen();
queen.eightQueen(0);
System.out.println("总共有 " +queen.count+ " 摆放方法");
}
总共有 92 摆放方法
2、约瑟夫环
1、问题描述
已知n个人(以编号1,2,3...n分别表示)围坐在一张圆桌周围。从编号为k的人开始报数,数到m的那个人出列;他的下一个人又从1开始报数,数到m的那个人又出列。依此规律重复下去,直到圆桌周围的人全部出列。
2、分析
这个就是约瑟夫环问题的实际场景,有一种是要通过输入n,m,k三个正整数,来求出列的序列。这个问题采用的是典型的循环链表的数据结构,就是将一个链表的尾元素指针指向队首元素
3、核心实现
1.建立一个具有n个链结点,无头结点的循环链表。
2.确定第1个报数人的位置。
3.不断地从链表中删除链结点,直到链表为空。
// 核心代码
while(current!=current.next){
// 至少还有两个人就仍然kill
for(int i=1;i<M;i++){
current=current.next;
}
System.out.println(current.next.val+"被kill掉了");
// 找下一个受害者
current.next=current.next.next;
}
第二种实现方案
现在假设m=10
0 1 2 3 4 5 6 7 8 9 k=3
第一个人出列后的序列为:
0 1 3 4 5 6 7 8 9
即:
3 4 5 6 7 8 9 0 1(*)
我们把该式转化为:
0 1 2 3 4 5 6 7 8 (**)
则你会发现: ((**)+3)%10则转化为(*)式了
也就是说,我们求出9个人中第9次出环的编号,最后进行上面的转换就能得到10个人第10次出环的编号了
设f(m,k,i)为m个人的环,报数为k,第i个人出环的编号,则f(10,3,10)是我们要的结果
当i=1时, f(m,k,i) = (m+k-1)%m
当i!=1时, f(m,k,i)= ( f(m-1,k,i-1)+k )%m
// 核心代码
private int ysf(int n,int m,int k){
if(k==1){
return (n+m-1)%n+1;
} else{
return (ysf(n-1,m,k-1)+m-1)%n+1;
}
}
第三种方案
数组中每个元素都是一个人,然后对数组进行循环处理,每当数组中的人数到m时,将其标记为淘汰。直到最后数组中只有一个人未被淘汰。
所以,首先,我们需要一个计算方法,参数中有总数和淘汰数两个参数。
private void function(int n,int m){}
第二步,我们需要一个长度为n的布尔值数组,数组的index就表示了第几个人,元素的true和false表示了这个人是否被淘汰。一开始我们需要将所有人都设置为未被淘汰。
boolean[] peopleFlags = new boolean[n];
for (int i = 0; i < n; i++) {
peopleFlags[i] = true;
}
接下来第三步,我们需要三个变量:
第一个变量记录还剩多少人为被淘汰,这个变量的初始值为总人数;
第二个变量记录数到了多少,当这个参数等于淘汰数时归零;
第三个参数记录当时数到了第几个人,当这个参数等于总人数时归零(因为是一个圈,所以最后一个人数完后又轮到第一个人数数)
int peopleLeft = n; //剩下的人数
int count = 0; //计数器,每过一个人加一,加到m时归零
int index = 0; //标记从哪里开始
第四步就开始循环计算了,首先判断剩余的人数是否大于一,如果大于一进入循环,取index,如果这个人未被淘汰,则计数器加一,如果等于m则淘汰这个人,否则跳过计数继续,当index等于总人数时
int peopleLeft = n; //剩下的人数
int count = 0; //计数器,每过一个人加一,加到keyNumber时归零
int index = 0; //标记从哪里开始
while (peopleLeft > 1) {
if (peopleFlags[index]) {
//说明还没有被淘汰 计数器加1
count++;
if (count == m) {
count = 0; //计数器归0
peopleFlags[index] = false; //此人被淘汰
peopleLeft--;//未被淘汰的人数-1
}
}
index++;
//当当前人等于总人数时,则又从第一人开始计数
if (index == n) {
index = 0;
}
}
最后,计算结束后,数组中只有一个元素为true,而这个就是最后没被淘汰的那个人,现在我们就开开始找到是谁赢得了这次比赛。
for (int j = 0; j < n; j++) {
if (peopleFlags[j]) {
alive =j+1;
}
}